In the past, the Earth's climate system appears to have moved sharply between colder and warmer modes. Can humanity risk the same at present from anthropogenic climate change? Honestly, climate models still cannot offer answers to that question.
 A brief overview of the findings. (Image Credit: TiPES/HP)
A brief overview of the findings. (Image Credit: TiPES/HP)
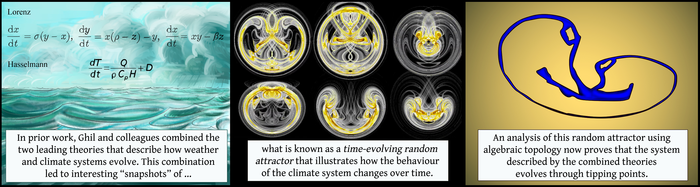
However, a finding in the journal Chaos by Gisela D. Charó, Denisse Sciamarella, Mickaël D. Chekroun and Michael Ghil proposes a technique to resolve the issue. Examining a model that integrates the two top theories for climate change with algebraic topology tools, the researchers demonstrate that the climate system certainly progresses through unexpected transitions, also referred to as tipping points.
These tools are pertinent to reduced climate models and they could possibly help evaluate whether the Earth's climate system in its entirety is about to tip because of global warming. The study is part of the TiPES project, a European science partnership on tipping points in the Earth system.
How Does the Climate Evolve?
It is one of the truly unsolved mysteries about the climate sciences, that we are trying to get at.
Michael Ghil, Study Researcher, École Normale Supérieure, Paris
There have been fundamentally two complementary opinions regarding what makes climate change. One is the inevitably chaotic opinion of Edward Lorenz. This is the chaos theory that is extensively known through the notion that the flapping of a butterfly’s wings on one continent can be the source of a powerful storm on another continent.
The other opinion is that of Klaus Hasselmann, a recent Nobel Prize winner, who stated that the climate system is stochastic and everything fluctuates but regresses to the mean.
The Combination Looks Strange
We have earlier, in 2008, brought these two theories together and shown that things get a lot more interesting if you have both deterministic chaos and stochastic perturbations.
Michael Ghil, Study Researcher, École Normale Supérieure, Paris
This random attractor shifts with time. The shape it acquires at a given instant, known as a snapshot, establishes where the climate system is most expected to be. It has not been direct, however, how to infer the random attractor’s shifts in time. What does its shifting path mean with regards to understanding the climate? Algebraic topology at present assists with that.
Abrupt changes
Algebraic topology is relatively abstract but its outcomes are easy to comprehend. If the geometric objects of the two systems are qualitatively similar, they possess the same number of holes.
The examination in Chaos of the climate’s random attractor exposes that, over time, holes appear and vanish. This means the system changes between diverse regimes. The changes seem to be sudden.
Since the analysis in effect exposes variations in the most central properties of the physical system being examined, the results indicate that the nature of Earth's climate undeniably is to change through sudden transitions — universally called tipping points.
Early Warning
The technique might have suggestions for forecasting the ultimate tipping of the climate system. At present, such tipping of the total climate system is a highly complicated occurrence to set up an early warning system for. However, algebraic topology could offer a solution.
This is a fairly robust method of establishing critical conditions in very complex situations. So I think that it should be possible to use these tools in order to really foreshadow transitions in a system that is as complex as the climate system.
Michael Ghil, Study Researcher, École Normale Supérieure, Paris
Success conducting this program, however, will rely on whether climate models can be minimized to manageable sizes for examination with the algebraic topology tools employed in this study.
Stochastic Strange Attractor
The result from 2008, a so-called random attractor, can be seen in the video. https://vimeo.com/240039610. Video Credit: University Of Copenhagen.
Journal Reference:
Charó, G. D., et al. (2021) Noise-driven topological changes in chaotic dynamics. Chaos: An Interdisciplinary Journal of Nonlinear Science. doi.org/10.1063/5.0059461.